Ilusiones #

‘Tienes que crear confusión sistemáticamente, libera la creatividad. Todo lo que es contradictorio crea vida’, Salvador Dalli

Penrose Triangle #

Historia #

El triángulo de Penrose fue creado por primera vez en 1934 por el pintor sueco Oscar Reutersvärd. Dibujó su versión de triángulo como un conjunto de cubos en proyección paralela. Aunque muchos pintores utilizaron triángulos imposibles en su arte, Oscar Reutersvärd abrió el mundo fantástico de las figuras imposibles. Creó miles de figuras imposibles para su vida y ahora se lo conoce como el “padre” de las figuras imposibles. En 1980, el gobierno sueco decidió colocar un triángulo imposible y otras dos figuras suyas en los sellos postales, que se imprimieron alrededor de dos años.

ImgEstampilla

En 1954, el matemático inglés Roger Penrose después de la lección del artista holandés M.C. Escher dibujó un triángulo imposible en su vista común. A diferencia del triángulo de Reutersvärd, pintó el triángulo como tres barras conectadas con ángulos rectos. Le dio un efecto de perspectiva, lo que aumentó el efecto de imposibilidad. Publicó su versión del triángulo en la revista British Psychology en 1954 en un artículo conjunto de él y su padre Lionel Penrose.

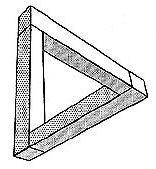
ImgPenrose

Mucha gente piensa que el triángulo de Penrose es realmente imposible y no se puede construir en el mundo real. Pero se demostró que todas las figuras imposibles son posibles de realizar. Es posible crear objetos tridimensionales que parezcan imposibles desde un único punto de vista y parezcan normales desde todos los demás puntos de vista. Un ejemplo de esta obra en la vida real, se encuentra en Australia, la cual es visitada por miles de turistas.

ImgPenroseAustralia

¿Por qué el triángulo de Penrose también es conocido como el triángulo imposible? #

Imposible porque aparenta ser un objeto sólido conformado por tres tramos rectos interconectados en los extremos del triángulo formando ángulos rectos, cosa que dentro de un espacio euclídeo ordinario no es posible la combinación de estas propiedades (aunque sí podría cumplirse dentro del espacio 3-variedad, campo el cual estudia variedades topológicas de tres dimensiones).

Estas y más son las razones del porqué su efecto visual causa gran impresión dentro de esta rama, y se ha catalogado como una de las ‘figuras imposibles’ que quedan definidas en imágenes de dos dimensiones, a las cuales se les agregan efectos para que luzcan imposibles tridimensionalmente. Pueden tener sentido dentro del plano 2D, pero no en el espacio 3D, por eso se denomina –según el investigador Abrahan Tamir en su estudio “geometría posible en 2D pero imposible en 3D” figura imposible al triángulo de Penrose.

Penrose Triangle 2D #

Code ...

function setup() {
  createCanvas(400, 400);
 
}

function draw() {
  background(0);
 
  stroke(175)
 
  noFill()
 
  strokeWeight(4)
 
  beginShape()
  vertex(187,100)
  vertex(100,217)
  vertex(118,235)
  vertex(281,235)
  vertex(292,217)
  vertex(209,100)
  vertex(188,100)
  vertex(255,198)
  vertex(223,198)
  //stroke(175)
  vertex(170,198)
  vertex(197,162)
  vertex(224,198)
  vertex(185,145)
  vertex(118,235)
  endShape()
 
  beginShape()
  vertex(170,198)
  vertex(157,217)
  vertex(292,217)
  endShape()
 
 
}

Penrose Triangle 3D #

Code ...

//penrose_triangle.js

let sf = 1; // scaleFactor
let locked = true;
function setup() {
  sliderx = createSlider(0, 10, 10, 0.1);
  sliderx.position(30, 30);

  slidery = createSlider(0, 10, 3.6, 0.1);
  slidery.position(30, 55);

  sliderz = createSlider(0, 10, 8.1, 0.1);
  sliderz.position(30, 80);

  createCanvas(700, 700, WEBGL);
  fill(237, 34, 93);

  cuboid1 = new Cuboid(0, 180, 0, 30, 0, 30);
  cuboid2 = new Cuboid(0, 30, 0, 30, 180);
  cuboid3 = new Cuboid(0, 30, 0, 120, 150, 30);
}

function draw() {
  scale(sf);
  background(200);
  rotateX(sliderx.value());
  rotateY(slidery.value());
  rotateZ(sliderz.value());

  // first cuboid 
  cuboid1.draw()
  //second cuboid
  cuboid2.draw()
  //third cuboid
  cuboid3.draw()

}

class Cuboid {
  constructor(x, w, y, h, z, d) {
    this.x = x
    this.w = w
    this.y = y
    this.h = h
    this.z = z
    this.d = d
  }

  draw() {
    
    beginShape();

    vertex(this.x, this.y, this.z);
    vertex(this.x + this.w, this.y, this.z);
    vertex(this.x + this.w, this.y + this.h, this.z);
    vertex(this.x, this.y + this.h, this.z);
    endShape(CLOSE);

    beginShape();
    vertex(this.x, this.y, this.z + this.d);
    vertex(this.x + this.w, this.y, this.z + this.d);
    vertex(this.x + this.w, this.y + this.h, this.z + this.d);
    vertex(this.x, this.y + this.h, this.z + this.d);
    endShape(CLOSE);

    beginShape();
    vertex(this.x + this.w, this.y, this.z);
    vertex(this.x, this.y, this.z);
    vertex(this.x, this.y, this.z + this.d);
    vertex(this.x + this.w, this.y, this.z + this.d);
    endShape(CLOSE);

    beginShape();
    vertex(this.x, this.y + this.h, this.z);
    vertex(this.x + this.w, this.y + this.h, this.z);
    vertex(this.x + this.w, this.y + this.h, this.z + this.d);
    vertex(this.x, this.y + this.h, this.z + this.d);
    endShape(CLOSE);

    beginShape();
    vertex(this.x, this.y, this.z);
    vertex(this.x, this.y, this.z + this.d);
    vertex(this.x, this.y + this.h, this.z + this.d);
    vertex(this.x, this.y + this.h, this.z);
    endShape(CLOSE);

    beginShape();
    vertex(this.x + this.w, this.y, this.z);
    vertex(this.x + this.w, this.y, this.z + this.d);
    vertex(this.x + this.w, this.y + this.h, this.z + this.d);
    vertex(this.x + this.w, this.y + this.h, this.z);
    endShape(CLOSE);
  }
}

function mousePressed() {
  locked = false
}

function mouseClicked() {
  //console.log('Released')
  locked = true
}

function mouseWheel(event) {
  if (locked != true) {
    if (event.deltaY < 0)
      sf *= 1.05;
    else
      sf *= 0.95;
  }
}

Penrose Staircase #

Code ...

function setup() {
    sliderx = createSlider(4, 7, 5.25, 0.01);
    sliderx.position(30, 30);

    slidery = createSlider(4, 7, 5.27, 0.01);
    slidery.position(30, 55);

    sliderz = createSlider(0, 10, 0, 0.01);
    sliderz.position(30, 80);

    createCanvas(700, 700, WEBGL);

    fill(237, 34, 93);

    //
    cuboid1 = new Cuboid(0, 50, 0, -(200 / 13) * 9, 0, 50);
    cuboid2 = new Cuboid(50, 50, 0, -(200 / 13) * 10, 0, 50);
    cuboid3 = new Cuboid(100, 50, 0, -(200 / 13) * 11, 0, 50);
    cuboid4 = new Cuboid(150, 50, 0, -(200 / 13) * 12, 0, 50);
    cuboid5 = new Cuboid(200, 50, 0, -(200 / 13) * 13, 0, 50);

    //  
    cuboid6 = new Cuboid(0, 50, 0, -(200 / 13) * 8, 0, -50);
    cuboid7 = new Cuboid(0, 50, (200 / 13) * 5, -(200 / 13) * 12, -50, -50);
    cuboid8 = new Cuboid(0, 50, (200 / 13) * 5, -(200 / 13) * 11, -100, -50);

    // 
    cuboid9 = new Cuboid(200, 50, 0, -(200 / 13) * 14, 0, -50);
    cuboid10 = new Cuboid(200, 50, 0, -(200 / 13) * 15, -50, -50);


    //
    cuboid11 = new Cuboid(150, 50, 0, -(200 / 13) * 16, -50, -50);
    //cuboid12 = new Cuboid(100, 50, -(200/13)*17, -(200/13)*1, -50, -50);


}

function draw() {

    scale(0.5);
    background(200);
    rotateX(sliderx.value());
    rotateY(slidery.value());
    rotateZ(sliderz.value());
    //console.log(sliderx.value()); 
    //console.log(slidery.value())
    //orbitControl()

    // first cuboid 
    cuboid1.draw()
    cuboid2.draw()
    cuboid3.draw()
    cuboid4.draw()
    cuboid5.draw()

    cuboid6.draw()
    cuboid7.draw()
    cuboid8.draw()

    cuboid9.draw()
    cuboid10.draw()
    cuboid11.draw()

    // frente
    // push son para modificar el estilo y no afectar el resto de la plantilla
    push()
    noStroke()
    beginShape();
    vertex(100, -(200 / 13) * 16, -50 - (200 / 13) * 2);
    vertex(150, -(200 / 13) * 16, -50 - (200 / 13) * 2);
    vertex(150, -(200 / 13) * 17, -50 - (200 / 13) * 1);
    vertex(100, -(200 / 13) * 17, -50 - (200 / 13) * 1);
    endShape(CLOSE);

    beginShape();
    vertex(100, -(200 / 13) * 16, -100);
    vertex(150, -(200 / 13) * 16, -100);
    vertex(150, -(200 / 13) * 17, -100);
    vertex(100, -(200 / 13) * 17, -100);
    endShape(CLOSE);
    pop()

    //inferior
    beginShape();
    vertex(150, -(200 / 13) * 16, -50 - (200 / 13) * 2);
    vertex(100, -(200 / 13) * 16, -50 - (200 / 13) * 2);
    vertex(100, -(200 / 13) * 16, -100);
    vertex(150, -(200 / 13) * 16, -100);
    endShape(CLOSE);

    //superior
    push()
    noStroke()
    beginShape();
    vertex(100, -(200 / 13) * 17, -50 - (200 / 13) * 1);
    vertex(150, -(200 / 13) * 17, -50 - (200 / 13) * 1);
    vertex(150, -(200 / 13) * 17, -100);
    vertex(100, -(200 / 13) * 17, -100);
    endShape(CLOSE);
    pop()

    // frente izq
    beginShape();
    vertex(100, -(200 / 13) * 16, -50 - (200 / 13) * 2);
    vertex(100, -(200 / 13) * 16, -100);
    vertex(100, -(200 / 13) * 17, -100);
    vertex(100, -(200 / 13) * 17, -50 - (200 / 13) * 1);
    endShape(CLOSE);

    // frente der
    beginShape();
    vertex(150, -(200 / 13) * 16, -50);
    vertex(150, -(200 / 13) * 16, -100);
    vertex(150, -(200 / 13) * 17, -100);
    vertex(150, -(200 / 13) * 17, -50);
    endShape(CLOSE);

    //triangle 
    push()
    noStroke()
    beginShape();
    vertex(150, -(200 / 13) * 17, -50 - (200 / 13) * 1)
    vertex(150, -(200 / 13) * 17, -50)
    vertex(150 - (200 / 13) * 1, -(200 / 13) * 17, -50 - (200 / 13) * 1)
    endShape(CLOSE);
    pop()
}

class Cuboid {
    constructor(x, w, y, h, z, d) {
        this.x = x
        this.w = w
        this.y = y
        this.h = h
        this.z = z
        this.d = d
    }

    draw() {

        beginShape();

        vertex(this.x, this.y, this.z);
        vertex(this.x + this.w, this.y, this.z);
        vertex(this.x + this.w, this.y + this.h, this.z);
        vertex(this.x, this.y + this.h, this.z);
        endShape(CLOSE);

        beginShape();
        vertex(this.x, this.y, this.z + this.d);
        vertex(this.x + this.w, this.y, this.z + this.d);
        vertex(this.x + this.w, this.y + this.h, this.z + this.d);
        vertex(this.x, this.y + this.h, this.z + this.d);
        endShape(CLOSE);

        beginShape();
        vertex(this.x + this.w, this.y, this.z);
        vertex(this.x, this.y, this.z);
        vertex(this.x, this.y, this.z + this.d);
        vertex(this.x + this.w, this.y, this.z + this.d);
        endShape(CLOSE);

        beginShape();
        vertex(this.x, this.y + this.h, this.z);
        vertex(this.x + this.w, this.y + this.h, this.z);
        vertex(this.x + this.w, this.y + this.h, this.z + this.d);
        vertex(this.x, this.y + this.h, this.z + this.d);
        endShape(CLOSE);

        beginShape();
        vertex(this.x, this.y, this.z);
        vertex(this.x, this.y, this.z + this.d);
        vertex(this.x, this.y + this.h, this.z + this.d);
        vertex(this.x, this.y + this.h, this.z);
        endShape(CLOSE);

        beginShape();
        vertex(this.x + this.w, this.y, this.z);
        vertex(this.x + this.w, this.y, this.z + this.d);
        vertex(this.x + this.w, this.y + this.h, this.z + this.d);
        vertex(this.x + this.w, this.y + this.h, this.z);
        endShape(CLOSE);
    }
}

Penrose Staircase Animation #

flex justify-between">Code class=hidden>

let a; i; setup() { a = [false, false, false, false, false, false, false, false, false, false, false, false] i = 0 sliderx = createSlider(4, 7, 5.25, 0.01); sliderx.position(30, 30); slidery = createSlider(4, 7, 5.27, 0.01); slidery.position(30, 55); sliderz = createSlider(0, 10, 0, 0.01); sliderz.position(30, 80); createCanvas(700, 700, WEBGL); fill(237, 34, 93); // cuboid1 = new Cuboid(0, 50, 0, -(200 / 13) * 9, 0, 50); cuboid2 = new Cuboid(50, 50, 0, -(200 / 13) * 10, 0, 50); cuboid3 = new Cuboid(100, 50, 0, -(200 / 13) * 11, 0, 50); cuboid4 = new Cuboid(150, 50, 0, -(200 / 13) * 12, 0, 50); cuboid5 = new Cuboid(200, 50, 0, -(200 / 13) * 13, 0, 50); // cuboid6 = new Cuboid(0, 50, 0, -(200 / 13) * 8, 0, -50); cuboid7 = new Cuboid(0, 50, (200 / 13) * 5, -(200 / 13) * 12, -50, -50); cuboid8 = new Cuboid(0, 50, (200 / 13) * 5, -(200 / 13) * 11, -100, -50); // cuboid9 = new Cuboid(200, 50, 0, -(200 / 13) * 14, 0, -50); cuboid10 = new Cuboid(200, 50, 0, -(200 / 13) * 15, -50, -50); // cuboid11 = new Cuboid(150, 50, 0, -(200 / 13) * 16, -50, -50); //cuboid12 = new Cuboid(100, 50, -(200/13)*17, -(200/13)*1, -50, -50); setTimeout(verdadero, 1000) style=color:#75715e>} draw() { scale(0.5); background(200); rotateX(sliderx.value()); rotateY(slidery.value()); rotateZ(sliderz.value()); //console.log(sliderx.value()); //console.log(slidery.value()) //orbitControl() if (a[0] == true) { console.log(a) push() translate(50 / 2, -(200 / 13) * 10, 50 / 2) sphere(10) pop() } if (a[1] == true) { push() translate(50 + 50 / 2, -(200 / 13) * 11, 50 / 2) sphere(10) pop() } if (a[2] == true) { push() translate(100 + 50 / 2, -(200 / 13) * 12, 50 / 2) sphere(10) pop() } if (a[3] == true) { push() translate(150 + 50 / 2, -(200 / 13) * 13, 50 / 2) sphere(10) pop() } if (a[4] == true) { push() translate(200 + 50 / 2, -(200 / 13) * 14, 50 / 2) sphere(10) pop() } if (a[5] == true) { push() translate(200 + 50 / 2, -(200 / 13) * 15, 50 / 2 - 50) sphere(10) pop() } if (a[6] == true) { push() translate(200 + 50 / 2, -(200 / 13) * 15, 50 / 2 - 100) sphere(10) pop() } if (a[7] == true) { push() translate(150 + 50 / 2, -(200 / 13) * 16, 50 / 2 - 100) sphere(10) pop() } if (a[8] == true) { push() translate(100 + 50 / 2, -(200 / 13) * 17, 50 / 2 - 100) sphere(10) pop() } if (a[9] == true) { push() translate(50 / 2, -(200 / 13) * 7, 50 / 2 - 150) sphere(10) pop() } if (a[10] == true) { push() translate(50 / 2, -(200 / 13) * 8, 50 / 2 - 100) sphere(10) pop() } if (a[11] == true) { push() translate(50 / 2, -(200 / 13) * 9, 50 / 2 - 50) sphere(10) pop() } // first cuboid cuboid1.draw() cuboid2.draw() cuboid3.draw() cuboid4.draw() cuboid5.draw() cuboid6.draw() cuboid7.draw() cuboid8.draw() cuboid9.draw() cuboid10.draw() cuboid11.draw() // frente // push son para modificar el estilo y no afectar el resto de la plantilla push() noStroke() beginShape(); vertex(100, -(200 / 13) * 16, -50 - (200 / 13) * 2); vertex(150, -(200 / 13) * 16, -50 - (200 / 13) * 2); vertex(150, -(200 / 13) * 17, -50 - (200 / 13) * 1); vertex(100, -(200 / 13) * 17, -50 - (200 / 13) * 1); endShape(CLOSE); beginShape(); vertex(100, -(200 / 13) * 16, -100); vertex(150, -(200 / 13) * 16, -100); vertex(150, -(200 / 13) * 17, -100); vertex(100, -(200 / 13) * 17, -100); endShape(CLOSE); pop() //inferior beginShape(); vertex(150, -(200 / 13) * 16, -50 - (200 / 13) * 2); vertex(100, -(200 / 13) * 16, -50 - (200 / 13) * 2); vertex(100, -(200 / 13) * 16, -100); vertex(150, -(200 / 13) * 16, -100); endShape(CLOSE); //superior push() noStroke() beginShape(); vertex(100, -(200 / 13) * 17, -50 - (200 / 13) * 1); vertex(150, -(200 / 13) * 17, -50 - (200 / 13) * 1); vertex(150, -(200 / 13) * 17, -100); vertex(100, -(200 / 13) * 17, -100); endShape(CLOSE); pop() // frente izq beginShape(); vertex(100, -(200 / 13) * 16, -50 - (200 / 13) * 2); vertex(100, -(200 / 13) * 16, -100); vertex(100, -(200 / 13) * 17, -100); vertex(100, -(200 / 13) * 17, -50 - (200 / 13) * 1); endShape(CLOSE); // frente der beginShape(); vertex(150, -(200 / 13) * 16, -50); vertex(150, -(200 / 13) * 16, -100); vertex(150, -(200 / 13) * 17, -100); vertex(150, -(200 / 13) * 17, -50); endShape(CLOSE); //triangle push() noStroke() beginShape(); vertex(150, -(200 / 13) * 17, -50 - (200 / 13) * 1) vertex(150, -(200 / 13) * 17, -50) vertex(150 - (200 / 13) * 1, -(200 / 13) * 17, -50 - (200 / 13) * 1) endShape(CLOSE); pop() style=color:#75715e>} create() { ellipse(56, 46, 55, 55); setTimeout(create, 1000); style=color:#75715e>} Cuboid { constructor(x, w, y, h, z, d) { this.x = x this.w = w this.y = y this.h = h this.z = z this.d = d } draw() { beginShape(); vertex(this.x, this.y, this.z); vertex(this.x + this.w, this.y, this.z); vertex(this.x + this.w, this.y + this.h, this.z); vertex(this.x, this.y + this.h, this.z); endShape(CLOSE); beginShape(); vertex(this.x, this.y, this.z + this.d); vertex(this.x + this.w, this.y, this.z + this.d); vertex(this.x + this.w, this.y + this.h, this.z + this.d); vertex(this.x, this.y + this.h, this.z + this.d); endShape(CLOSE); beginShape(); vertex(this.x + this.w, this.y, this.z); vertex(this.x, this.y, this.z); vertex(this.x, this.y, this.z + this.d); vertex(this.x + this.w, this.y, this.z + this.d); endShape(CLOSE); beginShape(); vertex(this.x, this.y + this.h, this.z); vertex(this.x + this.w, this.y + this.h, this.z); vertex(this.x + this.w, this.y + this.h, this.z + this.d); vertex(this.x, this.y + this.h, this.z + this.d); endShape(CLOSE); beginShape(); vertex(this.x, this.y, this.z); vertex(this.x, this.y, this.z + this.d); vertex(this.x, this.y + this.h, this.z + this.d); vertex(this.x, this.y + this.h, this.z); endShape(CLOSE); beginShape(); vertex(this.x + this.w, this.y, this.z); vertex(this.x + this.w, this.y, this.z + this.d); vertex(this.x + this.w, this.y + this.h, this.z + this.d); vertex(this.x + this.w, this.y + this.h, this.z); endShape(CLOSE); } style=color:#75715e>} verdadero() { a[i] = true if (i != 0) { a[i - 1] = false } else { a[11] = false } if (i == 11) { i = 0 } else { i++ } setTimeout(verdadero, 1000) style=color:#75715e>} l>