Proyecciones #
Para estas proyecciones y su interpretacion se basa en The Math behind (most) 3D games - Perspective Projection, Esta difiere de la implementacion vista en clase debido a que varia el View Volume y el sistema de coordenadas, pero la explicacion nos da una buena introducción a lo que se busca con las proyecciones
Para tener en cuenta esta usa el software vulkan q al igual que OpenGL tienen el objetivo de producir graficas en 3D
Nosotros en p5js usamos, WebGL is a web version on OpenGL, i.e a 3D engine. “It allows you to make 3D materials in the browser, using JavaScript. It is rendered using the GPU and thus is more performant than regular canvas, so it is also used for 2D games.” (Por lo que vemos que el sistema que usamos en clase es el mismo de OpenGL, asi que esto es simplemente demostrativo con otro caso)
Ahora bien en que difiere el View Volume de Vulkan con respecto al de OpenGL:
El de vulkan tiene las siguientes coordenadas que definen el cuboid:
$$\text{x from }(-1,1) $$
$$\text{y from }(-1,1)$$
$$\text{z from }(0,1)$$
Como hemos dicho difiere del de OpenGL en el hecho de que el view volume es diferente, ya que en el caso de OpenGL es un cubo, en el que z va de -1 a 1, ademas de que el sistema de coordenadas en OpenGL es zurdo, mientras este es derecho

Proyeccion Ortogonal (Analogo, para otro View Volume y diferente sistema de coordenadas) #
Una proyeccion ortogonal es una generalizacion del volumen de la vista que nos permite especificar las dimensiones y la ubicacion que queramos pero mantiene la forma general del volumen de la vista y mantiene fijas la direccion y la orientacion de la vista
En el caso de OpenGL:
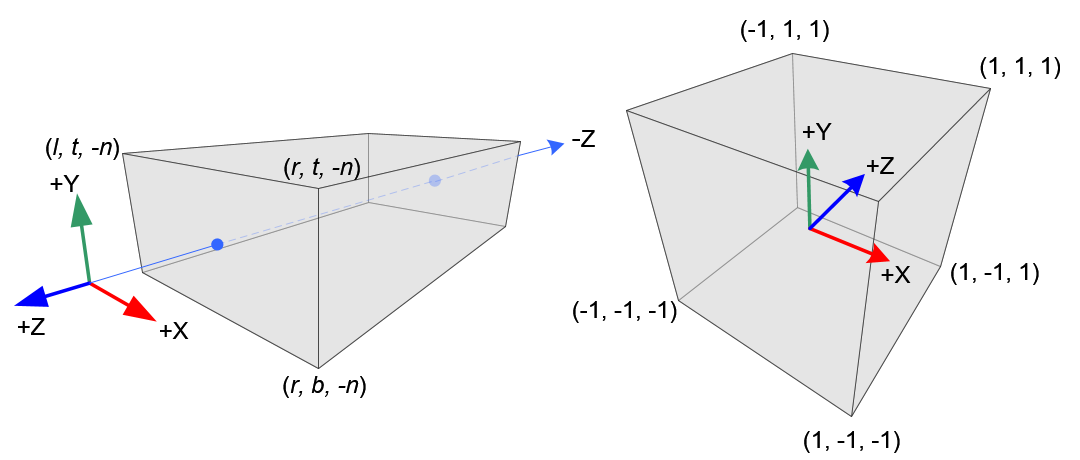
EN el caso de Vulkan:
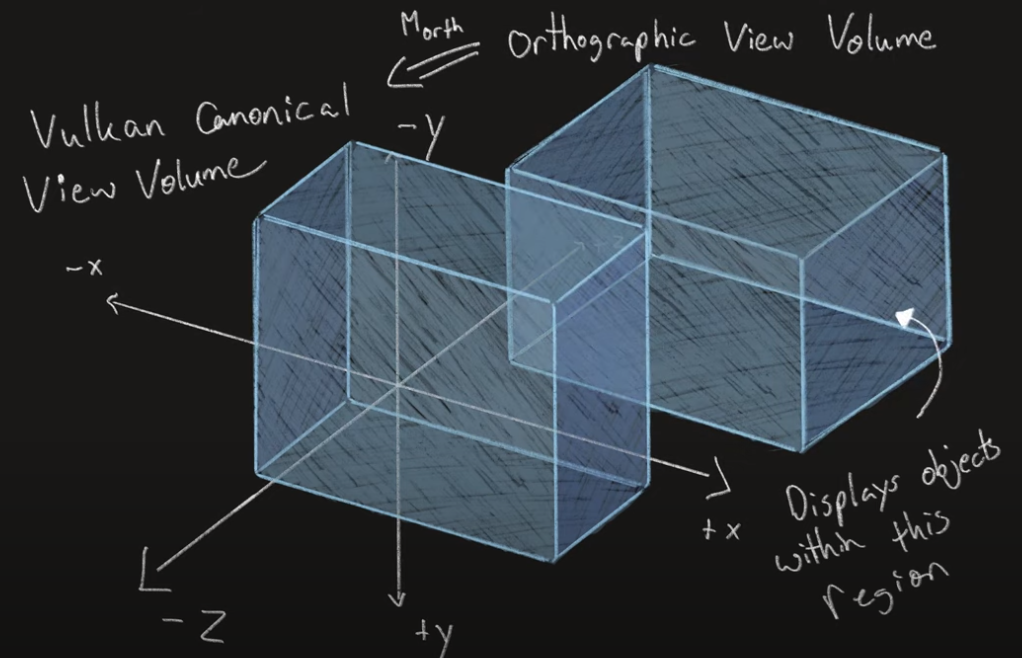
Ahora bien, continuando, lo que debemos hacer es:
Tener claro que el view volume tiene 6 planos que son right,left,top,bottom,far,near
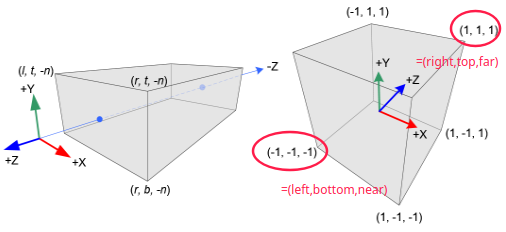
Volviendo al caso que estamos analizando:
- Translate centre c, of near plane to origin:
Translation Matrix: \[\text{Translation Matrix =}\begin{pmatrix} 1 & 0 & 0 & -C_x\\ 0 & 1 & 0 & -C_y\\ 0 & 0 & 1 & -C_z\\ 0 & 0 & 0 & 1 \end{pmatrix}\]
Reemplazando \[ \text{Translation Matrix=} \begin{pmatrix} 1 & 0 & 0 & -(r+l)/2\\ 0 & 1 & 0 & -(b+t)/2\\ 0 & 0 & 1 & -n\\ 0 & 0 & 0 & 1 \end{pmatrix}\]
- Scale Matrix to size of canonical
Ahora bien en esta matriz para escalar es importante tener en cuenta que en los primeros 3 valores de la diagonal principal de la matriz, el numerador hace referencia a las dimensiones del view volume, en este caso (2,2,1), en el caso de OpenGL seria (2,2,2)
\[M_{ort}=\begin{pmatrix}
\frac{2}{S_x} & 0& 0 & 0\\
0 & \frac{2}{S_y} & 0 & 0\\
0 & 0 & \frac{1}{S_z} & 0\\
0 & 0 & 0 & 1
\end{pmatrix}\begin{pmatrix}
1 & 0 & 0 & -(r+l)/2\\
0 & 1 & 0 & -(b+t)/2\\
0 & 0 & 1 & -n\\
0 & 0 & 0 & 1
\end{pmatrix}\]
Y el denominador van a ser las dimensiones del View Volume ortogonal
\[M_{ort}=\begin{pmatrix}
\frac{2}{(r-l)} & 0 & 0 & 0\\
a & \frac{2}{(b-t)} & 0 & 0\\
0 & 0 & \frac{1}{f-n} & 0\\
0 & 0 & 0 & 1
\end{pmatrix}\begin{pmatrix}
1 & 0 & 0 & -(r+l)/2\\
0 & 1 & 0 & -(b+t)/2\\
0 & 0 & 1 & -n\\
0 & 0 & 0 & 1
\end{pmatrix}=\begin{pmatrix}
\frac{2}{(r+l)} & 0 & 0 & \frac{-(r-l)}{(r-l)}\\
0 & \frac{2}{(b-t)} & 0 & \frac{-(b+t)}{(b-t)}\\
0 & 0 & \frac{1}{(f-n)} & \frac{-n}{(f-n)}\\
0 & 0 & 0 & 1
\end{pmatrix}\]
Al aplicar estas transformaciones a nuestros objetos, los objetos que se encuentran dentro de la region ocupada por el volumen de vista ortografica se escalaran y se moveran a la region cubierta por el volumen de vista canonica, y por lo tanto los !objetos se mostraran¡
Matriz de perspectiva (OpenGL) #
Pero el volumen de la vista ortografica no aplica la perspectiva, para ello necesitamos un volumen de visualizacion que no tenga forma de caja, sino una forma conocida como Square Frustrum
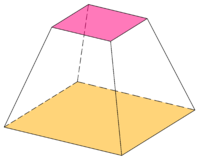
La idea del frustum cuadrado en la proyeccion es:
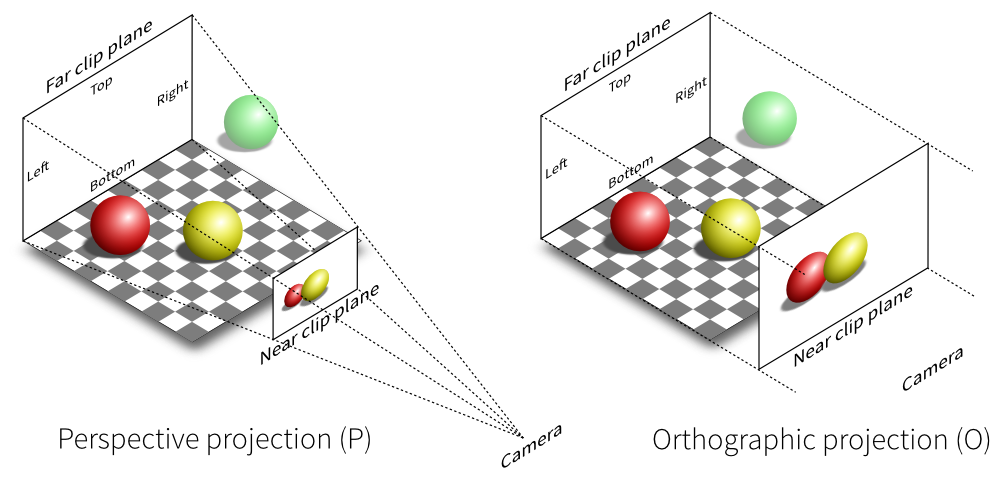
Entonces lo que queremos es una matriz de perspetiva que transforme el tronco y cualquier objeto que contenga en el volumen de la vista Ortogonal
Para ello es imporante la siguiente notación:
Ya entendido el concepto vamos a mostrar este ejemplo con la de OpenGL:
En OpenGL la matriz de perspectiva esta definida como: \[\left[\begin{array}{cccc} { \dfrac{2n}{ r-l } } & 0 & { \dfrac{r + l} { r-l } } & 0 \\ 0 & { \dfrac{2n}{ t-b } } & { \dfrac{t + b}{ t-b } } & 0 \\ 0 & 0 & -{\dfrac{f+n}{f-n}} & -{\dfrac{2fn}{f-n}}\\ 0 & 0 & -1& 0\\ \end{array}\right]\]
Para empezar es importante recordar que las matrices en OpenGL, estan definidas usando Column Major Order
Cuando multiplicamos un punto homogéneo con esta matriz, la coordenada w del punto se multiplica por este elemento y el valor de w resulta ser la coordenada z del punto proyectado
Principio de esto: Podemos usar el truco de triangulos similares. los triangulos A B C y D E F son similares. Por lo tanto podemos escribir:
Si reemplazamos AB por n, el plano de recorte cercano, DE con Pz(la coordenada z de P) y EF con Py(la coordenada y de P) podemos reescribir esta ecuación como (ecuación 1): \[{\dfrac{n}{-P_z}} = {\dfrac{BC}{P_y}} \rightarrow BC = Ps_y = {\dfrac{n * P_y}{-P_z}}.\]
Ahora bien aca podemos hacer el razonamiento de que (tenga en cuenta que debido a que la cámara está orientada a lo largo del eje z negativo,Pz es negativo:Pz< 0. Para mantener positiva la coordenada y del punto proyectado, ya que Py es positivo, tenemos que Pz). Si seguimos el mismo razonamiento encontramos la coordenada x del punto proyectado usando la siguiente ecuación: \[Ps_x =\dfrac{n * P_x}{-P_z}.\]
Ahora bien debemos relacional Psx y psy con la matriz de perspectiva.
Si asumimos que Ps es visible, podemos escribir: \[l \leq Ps_x \leq r.\] donde l=left y r= right
Comencemos eliminando l de todos los términos y reescribiendo la ecuación anterior como: \[0 \leq Ps_x - l \leq r - l.\] Podemos normalizar dividiendo todos los perminos por r-l: \[0 \leq {\dfrac{Ps_x - l}{r-l}} \leq 1.\]
Multiplicamos los teminos por 2: \[0 \leq 2{\dfrac{Ps_x - l}{r-l}} \leq 2.\]
removiendo el -1 de todos los terminos: \[-1 \leq 2{\dfrac{Ps_x - l}{r-l}} -1 \leq 1.\]
Ahora remapeamos el termino central al rango [-1,1]:
\[-1 \leq 2{ \dfrac{Ps_x - l}{r-l} } - { \dfrac{r-l}{r-l} } \leq 1.\]Teniendo: \[-1 \leq { \dfrac{2Ps_x - 2l - r + l}{r-l} } \leq 1.\]
Por lo tanto: \[-1 \leq { \dfrac{2Ps_x - l - r}{r-l} } \leq 1 \rightarrow -1 \leq { \dfrac{2Ps_x}{r-l} } - { \dfrac{r + l}{r - l} } \leq 1.\]
esos dos terminos son similares a los 2 primeros de la primera fila de OpenGL perspective projection matrix, estamos cerca, por lo que reemplazamos Psx de la ecuacion previa con la ecuacion 2, teniendo: \[-1 \leq { \dfrac{2 n P_x}{-P_z{(r-l)}} } - { \dfrac{r + l}{r - l} } \leq 1.\]
Podemos facilmente ponerlo en forma de matriz \[ \left[\begin{array}{cccc} { \dfrac{2n}{ r-l } } & 0 & { \dfrac{r + l}{ r-l } } & 0 \\ ... & ... & ... & ... \\ ... & ... & ... & ... \\ 0 & 0 & -1& 0\\ \end{array}\right] \]
Recordando la notacion de multiplicacion por vectores columna de OpenGL: \[\left[\begin{array}{cccc} { \dfrac{2n}{ r-l } } & 0 & { \dfrac{r + l}{ r-l } } & 0 \\ ... & ... & ... & ... \\ ... & ... & ... & ... \\ 0 & 0 & -1& 0\\ \end{array}\right] * \left[ \begin{array}{cccc}x \\ y \\ z \\ w\end{array}\right]\]
Computando Psx, usando las matrices dadas: \[Ps_x = { \dfrac{2n}{ r-l } } P_x + 0 * P_y + { \dfrac{r + l}{ r-l } } * P_z + 0 * P_w.\]
Convirtiendo Ps de homogenea a coordenadas cartesianas: \[Ps_x = \dfrac { \dfrac {2n} { r-l } P_x } { -P_z} + \dfrac{ \dfrac {r + l} { r-l } P_z } { -P_z} \rightarrow \dfrac {2n P_x} { -P_z (r-l) } - \dfrac {r + l} { r-l }.\]
Reemplazando l y r con b y t: \[-1 \leq { \dfrac{2 n P_y}{-P_z{(t-b)}} } - { \dfrac{t + b}{t - b} } \leq 1.\]
Podemos obtener este resultado con una multiplicación matricial puntual si reemplazamos los coeficientes segundo y tercero de la segunda fila de la matriz con el primer y segundo término de esta ecuación:
\[\left[\begin{array}{cccc} { \dfrac{2n}{ r-l } } & 0 & { \dfrac{r + l}{ r-l } } & 0 \\ 0 & { \dfrac{2n}{ t-b } } & { \dfrac{t + b}{ t-b } } & 0 \\ ... & ... & ... & ... \\ 0 & 0 & -1& 0\\ \end{array}\right]\]Computando Psy usando las matrices dadas:
\[Ps_y = 0 * P_x + { \dfrac{2n}{ (t-b) } } * P_y + { \dfrac{t + b}{ t-b } } * P_z + 0 * P_w\]Y despues de la division por -Pz: \[Ps_y = \dfrac { \dfrac {2n} {t - b} P_y } { -P_z} + \dfrac{ \dfrac {t + b} {t - b} P_z } { -P_z} \rightarrow \dfrac {2n P_y} { -P_z (t - b) } - \dfrac {t + b} {t - b}\]
La matriz vuelve a funcionar, y Por lo tanto, los coeficientes primero y segundo de la tercera fila de la matriz, que se multiplicarían por las coordenadas P x e y, son necesariamente cero (en verde). Nos quedan dos coeficientes A y B en la matriz que son desconocidos (en rojo). \[\left[\begin{array}{cccc} { \dfrac{2n}{ r-l } } & 0 & { \dfrac{r + l}{ r-l } } & 0 \\ 0 & { \dfrac{2n}{ t-b } } & { \dfrac{t + b}{ t-b } } & 0 \\ \color{green}0 & \color{green}0 & \color{red}A & \color{red}B \\ 0 & 0 & -1& 0\\ \end{array}\right]\]
Si escribimos las ecuacion para computar Psz (recordando que Psz se divide tambien por Psw, cuando el punto es convertido de homogenea a cooredeandas cartesianas, y que Pw=1): \[Ps_z = \dfrac{0 * P_x + 0 * P_y + A * P_z + B * P_w}{Ps_w = -P_z} \rightarrow \dfrac{A P_z + B}{Ps_w = -P_z}.\]
Necesitamos encontrar el valor de A y B. Con suerte sabemos que cuando Pz encuentra en el plano de recorte cercano,Psz ser reasignado a -1 y Pz encuentra en el plano de recorte lejano,Psz necesita ser reasignado a 1. Por lo tanto, necesitamos reemplazar Psz por n y f la ecuación para obtener dos nuevas ecuaciones (tenga en cuenta que la coordenada z de todos los puntos proyectados en el plano de la imagen son negativas pero n y F son positivos por lo tanto usaremos -n y -f cambio): \[\left\{ \begin{array}{ll} \dfrac{(P_z=-n)A + B}{(-P_z=-(-n)=n)} = -1 &\text{ when } P_z = n\\ \dfrac{(P_z=-f)A + B}{(P_z=-(-f)=f)} = 1 & \text{ when } P_z = f \end{array} \right. \\ \rightarrow \left\{ \begin{array}{ll} {-nA + B} = -n & (1)\\ {-fA + B} = f & (2) \end{array} \right.\]
Resolviendo B en la ecuacion 1: \[B = -n + An.\]
Sustituyendo B en la ecuacion 2, con est ecuacion: \[-fA - n + An = f. \]
Luego resolviendo A: \[-fA + An = f + n \rightarrow -(f - n)A = f + n \rightarrow A = -\dfrac{f + n}{f - n}. \]
Ya que tenemos la solucion para A, es facil encontrar B, solo necesitamos reemplazar A en la ecuacion 1 para encontrar B: \[B = -n + An= -n -\dfrac{f + n}{f - n} n = \\-(1+\dfrac{f + n}{f - n}) n = - \dfrac{{(f -n + f + n)}n}{f - n}=-\dfrac { 2fn }{f -n}\]
Hallado A y B, finalmente tenemos que \[\left[\begin{array}{cccc} { \dfrac{2n}{ r-l } } & 0 & { \dfrac{r + l}{ r-l } } & 0 \\ 0 & { \dfrac{2n}{ t-b } } & { \dfrac{t + b}{ t-b } } & 0 \\ 0 & 0 & -{\dfrac{f+n}{f-n}} & -{\dfrac{2fn}{f-n}}\\ 0 & 0 & -1& 0\\ \end{array}\right]\]